The essence of the first law of thermodynamics is energy conservation. We need to understand different forms of energy in a system. Internal energy, kinetic energy, and potential energy constitute the total stored energy of a system if the system is free of magnetic, electric, and surface tension effects.

\[E=U+KE+PE\]

where

\[E\]

\[KE\]

\[PE\]

\[U\]

Internal energy is associated with the motions and structure of the molecules of a system in a microscopic level. A system, no matter how tiny it is, contains a significantly large number of molecules in various modes of random motions, such as translation, rotation, and vibration. Although it is difficult to predict the behaviour of individual molecules, the statistical average can be calculated by using statistical theory. From a statistical standpoint, the internal energy of a system is considered to be the sum of the kinetic and potential energies of the collection of all molecules in the system. Maxwell explains the relation between the molecular velocity (a microscopic quantity) and the temperature (a macroscopic quantity) of a gas: as the temperature increases, the gas molecules move faster causing the mean microscopic kinetic energy of all molecules to increase; therefore, the internal energy of the system increases. In other words, the internal energy of a substance is strongly associated with the temperature of the substance; therefore, internal energy is a form of thermal energy. For example, the internal energy of 1 kg of water at 500 kPa increases from about 83.88 kJ to 167.47 kJ when its temperature increases from 20oC to 40oC. In general, temperature has a dominant effect on the internal energy of a system although other factors, such as pressure, phase, and chemical composition may also have an effect on the internal energy of a system.

From a macroscopic standpoint, a thermodynamic system, as a whole, has both kinetic and potential energies when it is in motion and is positioned at an elevation on Earth. The kinetic and potential energies are two forms of mechanical energy. They must be described with respect to an external reference frame. When a system experiences a change of elevation or velocity, the kinetic and potential energies of the system will convert between each other. For example, a rock falling from a cliff gains kinetic energy but losses potential energy because its elevation decreases with respect to the ground.

In general, the total stored energy of a thermodynamic system consists of the internal, kinetic, and potential energies. However, the kinetic and potential energies are insignificant compared to the internal energy in many cases, and thus can be neglected.

\[E, U, KE\]

\[e=u+ke+pe\]

where

: total specific energy, in J/kg or kJ/kg

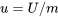: specific internal energy, J/kg or kJ/kg

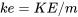: specific kinetic energy, J/kg or kJ/kg

: specific potential energy, J/kg or kJ/kg

The internal energy and specific internal energy are important properties for the analysis of closed systems, which will be explained in detail in Chapters 4-6.

Enthalpy is an important thermodynamic property for the analysis of open systems or control volumes, where mass transfer is always accompanied by energy transfer. Enthalpy is calculated as the sum of the internal energy, 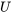, and the flow work, 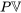, of the fluid flowing into or out of a control volume.

\[H=U+P\mathbb V\]

Now, what is flow work and why is it written as 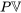? Let us consider a fluid element entering a control volume of a pipe section, see Figure 2.2.4. The control volume is illustrated as the red, dashed-lined rectangle. The fluid element, just before it enters the control volume, is at an equilibrium state and has an internal energy, 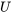, and a pressure, 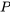. The fluid element carries its internal energy as it flows into the control volume. In addition, the fluid element must overcome the resistance from the downstream flow in the pipe. In other words, a certain amount of work must be done to force the fluid element into the control volume. We call such work essential to maintain the continuous flow of a fluid through a control volume as flow work. Refer to Figure 2.2.4, the flow work can be calculated as

\[W_{flow \, work} = FL =(PA)L =P(AL) =P\mathbb V\]

where 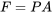is the pressure force acting on the cross-section, or the left control surface, of the control volume. 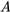is the cross-sectional area of the left control surface. is the distance that the fluid element travels from its original position to where it just enters the control volume completely. 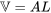is the volume of the fluid element.

For flow through an open system or control volume, both the internal energy carried by the fluid throughout the flow and the flow work required to maintain the flow contribute to the change of energy in a control volume. Therefore, it is common to combine the internal energy and the flow work as a new thermodynamic property, enthalpy, .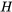

Enthalpy, similar to the internal energy, is an extensive property because its value depends on the mass of a system. Its corresponding intensive property is called specific enthalpy, or enthalpy per unit mass of a substance.

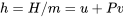
where

\[h\]

\[H\]

\[m\]

\[P\]

\[u\]

\[v\]

Some processes occur spontaneously in nature, such as salt dissolving in water. But some processes cannot occur spontaneously in nature. For example, water at 80oC and 10oC can mix in a container and eventually reach a thermal equilibrium. The mixture, however, cannot separate spontaneously into water at 80oC and water at 10oC. In other words, the process of separating the mixture is “irreversible” and cannot happen spontaneously. We may use a thermodynamic property called entropy to help us understand the physics of such phenomena.

Entropy is a measure of the lack of order resulting from the dispersal of energy and matter. Every spontaneous process is accompanied by an increase in the entropy (or disorder) of the universe. From a statistics point of view, it is more probable that the dispersal of energy and matter in a process is rather “random” than “orderly”. If we consider a fixed amount of gas in an isolated container, as illustrated in Figure 2.2.5. The probability of the molecules having a random distribution is much higher than the probability of them having an “orderly” distribution. Entropy is a concept to represent the degree of the “randomness” or “disorder” of a system. Such “disorder” was explained in statistical theories by early scientists such as Maxwell, Boltzmann, and Gibbs. Nowadays, entropy has been generally recognized as an important thermodynamic property associated with the “quality” aspect of the energy of a system; while energy represents the “quantity” aspect of the energy of the system. Both energy and entropy are of great importance in thermal analysis. The first law of thermodynamics, see Chapters 4 and 5, addresses the concepts of energy and energy conservation. The second law of thermodynamics is closely associated with the concepts of entropy and entropy generation, which explain why a process in nature only occurs in the direction of decreasing the quality of energy or increasing the entropy of the universe. These concepts will be explained in detail as we study the second law of thermodynamics in Chapter 6.

Entropy, 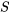, is an extensive property as its value depends on the mass of a system. The common SI units for entropy include kJ/K and J/K. Its corresponding intensive property is called specific entropy, 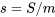. Its common SI units are kJ/kgK or J/kgK.

Query \(\PageIndex{1}\)

Query \(\PageIndex{2}\)